2 Deck Blackjack Vs 6 Deck
Let's consider card counting on a blackjack game with 6 decks of cards. This is one of the most popular games at online and land casinos, but, do not forget that it is impossible to count cards online. The table and the graphics below show you how likely the counts are and what your winning odds will be.
Here's the situation: Us: 6,6 Them: 2. Here's the situation - you're playing a multiple deck game where DDAS (doubling down after split) is available. You've been dealt a pair of sixes and the dealer has a two showing. That's always a tough card to play against, and not to be taken lightly. What is the right way. All of which explains, incidentally, why a one-deck game with a 6-to-5 blackjack payoff a paltry 20 percent bonus is a bum deal. Similar arithmetic shows doubles to be stronger in six- than eight-deck games.
% of times occurred in the games
Count
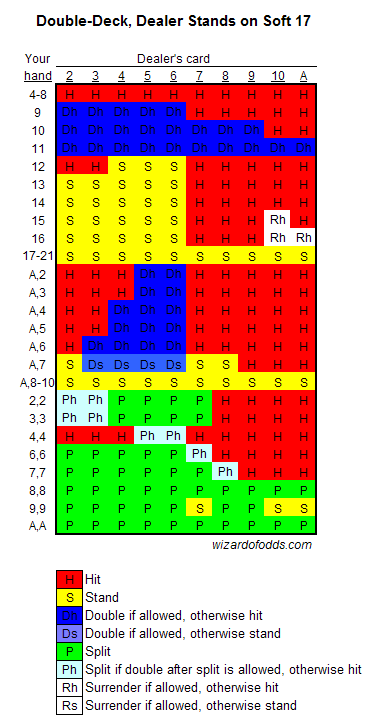
The most probable count to occur is a 'zero' count, however, sometimes differences occur and the table below shows just how.
| Count | % | Prob. this or more |
| -39 | 0,00000008% | 100,00000000% |
| -38 | 0,00000020% | 99,99999992% |
| -37 | 0,00000052% | 99,99999972% |
| -36 | 0,00000168% | 99,99999920% |
| -35 | 0,00000480% | 99,99999752% |
| -34 | 0,00000888% | 99,99999272% |
| -33 | 0,00001664% | 99,99998384% |
| -32 | 0,00003104% | 99,99996720% |
| -31 | 0,00006028% | 99,99993616% |
| -30 | 0,00011232% | 99,99987588% |
| -29 | 0,00021916% | 99,99976356% |
| -28 | 0,00038904% | 99,99954440% |
| -27 | 0,00072388% | 99,99915536% |
| -26 | 0,00124204% | 99,99843148% |
| -25 | 0,00207156% | 99,99718944% |
| -24 | 0,00349764% | 99,99511788% |
| -23 | 0,00577516% | 99,99162024% |
| -22 | 0,00930460% | 99,98584508% |
| -21 | 0,01452172% | 99,97654048% |
| -20 | 0,02270716% | 99,96201876% |
| -19 | 0,03450448% | 99,93931160% |
| -18 | 0,05066440% | 99,90480712% |
| -17 | 0,07535312% | 99,85414272% |
| -16 | 0,10798116% | 99,77878960% |
| -15 | 0,15243196% | 99,6708% |
| -14 | 0,21385236% | 99,5184% |
| -13 | 0,29419912% | 99,3045% |
| -12 | 0,39597112% | 99,0103% |
| -11 | 0,51736804% | 98,6144% |
| -10 | 0,70998200% | 98,1% |
| -9 | 0,90099252% | 97,4% |
| -8 | 1,17157960% | 96,5% |
| -7 | 1,56993548% | 95,3% |
| -6 | 2,06477432% | 93,7% |
| -5 | 2,76675644% | 91,7% |
| -4 | 3,80111092% | 88,9% |
| -3 | 5,44246824% | 85,1% |
| -2 | 8,15994788% | 79,7% |
| -1 | 13,10684724% | 71,5% |
| 0 | 16,83048012% | 58,4% |
| 1 | 13,10062740% | 41,6% |
| 2 | 8,15290812% | 28,5% |
| 3 | 5,43519040% | 20,3% |
| 4 | 3,79563692% | 14,9% |
| 5 | 2,76242648% | 11,1% |
| 6 | 2,06040976% | 8,3% |
| 7 | 1,56590072% | 6,3% |
| 8 | 1,16980792% | 4,7% |
| 9 | 0,90060712% | 3,5% |
| 10 | 0,71019488% | 2,6% |
| 11 | 0,51824868% | 1,9184% |
| 12 | 0,39732080% | 1,4002% |
| 13 | 0,29588316% | 1,0028% |
| 14 | 0,21550572% | 0,7069% |
| 15 | 0,15408880% | 0,4914% |
| 16 | 0,10962696% | 0,33735420% |
| 17 | 0,07674228% | 0,22772724% |
| 18 | 0,05193564% | 0,15098496% |
| 19 | 0,03565008% | 0,09904932% |
| 20 | 0,02349176% | 0,06339924% |
| 21 | 0,01506204% | 0,03990748% |
| 22 | 0,00968112% | 0,02484544% |
| 23 | 0,00603992% | 0,01516432% |
| 24 | 0,00371720% | 0,00912440% |
| 25 | 0,00223572% | 0,00540720% |
| 26 | 0,00135436% | 0,00317148% |
| 27 | 0,00079580% | 0,00181712% |
| 28 | 0,00044736% | 0,00102132% |
| 29 | 0,00026556% | 0,00057396% |
| 30 | 0,00014268% | 0,00030840% |
| 31 | 0,00007744% | 0,00016572% |
| 32 | 0,00004188% | 0,00008828% |
| 33 | 0,00002460% | 0,00004640% |
| 34 | 0,00001232% | 0,00002180% |
| 35 | 0,00000588% | 0,00000948% |
| 36 | 0,00000272% | 0,00000360% |
| 37 | 0,00000084% | 0,00000088% |
| 38 | 0,00000004% | 0,00000004% |